Clicca qui

Scrivere l’equazione della sfera  S  avente il centro nel piano  e  tangente in  al piano .

Clicca qui

Data la sfera  S )

a) scrivere l’equazione del piano tangente alla sfera in ,

b) data la retta   

scrivere le equazioni della retta  parallela ad  e passante per il centro di  S .

Clicca qui

Scrivere l’equazione della sfera avente il centro nel punto

 e soddisfacente ad una delle seguenti condizioni:

a) il raggio è 3;

b) S  passa per il punto ;

c) S  è tangente al piano .

.

Trovare l’equazione della sfera  S  avente il centro  e sia tangente alla retta

Clicca qui

Determinare le equazioni della retta tangente in  alla sfera di equazione

e che interseca la retta

.

Clicca qui

Determinare le equazioni delle sfere tangenti ai piani coordinati  e ,

 passanti per i punti  e .

Clicca qui

Determinare l’equazione della sfera tangente in  

al piano passante per  e per la retta

e avente il centro nel piano .

Clicca qui

Dati i punti

,  ,  ,  ,

determinare l’equazione della sfera di centro  e tangente al piano che passa per  A, B, C .

Clicca qui

Data la sfera

e il piano , determinare le equazioni dei piani tangenti a  paralleli a .

Clicca qui

Determinare le equazioni della retta tangente alla sfera di equazione

nel punto  e ortogonale alla retta

.

Clicca qui

Dati i punti

,  ,    

determinare la sfera che passa per  A, B, C  ed avente il centro sulla retta .

Clicca qui

Tra tutte le sfere tangenti al piano  nel punto   

determinare quella tangente alla sfera .

Clicca qui

Determinare le equazioni delle sfere tangenti al piano

  nel punto  e tangenti alla retta  .

Clicca qui

Date le equazioni delle tre rette

sono complanari? Se sì, scrivere l’equazione del piano che contiene tutte e tre le rette.

Calcolare l’equazione della sfera tangente alle tre rette.
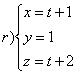
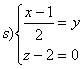