Esercizio:
Descrizione:
|
|
Determinare la
retta per P parallela al piano a
e che interseca la retta r.
|
|

|
1) Verificare che tali rette
sono perpendicolari e incidenti in P
2)scrivere
l’equazione del piano individuato da r1 ed r2
e verificare che tale piano è ^ a OP
|
|
|
1) verificare che la retta r
appartiene al piano p
2) scrivere l’equazione del
piano per r ^ a p .
3) scrivere l’equazione del
piano passante per P e // a p
|
|
Nello spazio S3 ,
riferito a un sistema cartesiano ortonormale, sono date le rette
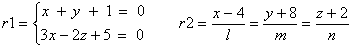
|
1) determinare la condizione per
cui le due rette sono complanari
2) determinare la condizione per
cui le due rette sono ^ .
3) determinare, nelle condizioni
previste ai punti 1) e 2), il punto di intersezione delle due rette
|
|
Nello spazio S3 ,
riferito a un sistema cartesiano ortonormale, sono dati
|
1) scrivere l’equazione del
piano p’ contenente
l’origine O, il punto P(2, 0, 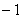 ), ^ al piano p ), ^ al piano p
2) verificare che r1
ed r2 sono complanari e determinare l’equazione del piano p” da esse individuato.
3) determinare l’angolo dei
piani p’ e p”
|
|
Nello spazio S3 , riferito a un sistema
cartesiano ortonormale, sono dati
|
1) scrivere l’equazione del piano p per B e per la retta per A
che si appoggia ^ alla retta r
2) scrivere l’equazione della retta t ^ alle rette r e AB (retta
di minima distanza)
3) determinare la minima distanza tra r e AB
|
|
Date le rette:
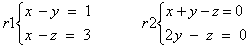
metodo 1°
metodo 2°
|
Determinare una
coppia di piani paralleli che le contengono.
|
|

|
Scrivere le
equazioni della retta
parallela al
vettore 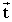 (1,-4
, 4) (1,-4
, 4)
e incidente
entrambe le rette.
Determinare la
distanza della retta
trovata dal punto P(1,
2, 3).
|
|
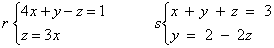
|
Scrivere le
equazioni della retta di minima distanza tra le rette.
|
|
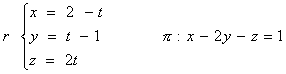
1° metodo
2° metodo
|
Scrivere le equazioni
parametriche di una retta r’ passante per P(5, 0, 1), // al
piano p e ortogonale alla
retta r .
Inoltre dire se le rette r ed
r’ sono sghembe.
|
|
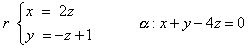
1° metodo
2° metodo
|
Scrivere le equazioni della
retta t
--perpendicolare e incidente
alla retta r
-- parallela al piano a
-- complanare con la retta s
che congiunge i punti:
P(0 ,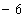 , ,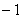 ) e Q(0
, ) e Q(0
,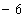 ,
1) ,
1)
|
|
|
Scrivere l’equazione del piano 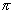 per il punto per il punto 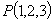 e parallelo
alle rette e parallelo
alle rette
|
|
|
Dati i punti A(0,0,1) , B(1,2,0)
e la retta r determinare :
a)l’equazione della retta s
per A incidente e ortogonale alla
retta r
b) l’equazione del piano 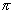 contenente
sia B che s contenente
sia B che s
c)la minima distanza tra la
retta r e la retta AB, nonché la equazioni della retta di
minima distanza corrispondente.
|
|
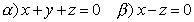
|
Dato il punto 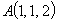 e i piani a e b
determinare la retta r) parallela ad entrambi i piani e passante per A.
Quanto dista questa retta dall’origine? e i piani a e b
determinare la retta r) parallela ad entrambi i piani e passante per A.
Quanto dista questa retta dall’origine?
|
|
|
Discutere, al variare di 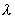 e e 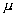 la reciproca
posizione delle due rette la reciproca
posizione delle due rette
|
|
|
Dati i punti 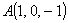 e e 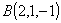 e la retta
r) e la retta
r)
a) verificare che le rette 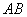 ed ed 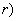 sono
incidenti, trovare il punto comune e l’equazione sono
incidenti, trovare il punto comune e l’equazione
del piano che le contiene;
b) determinare il punto 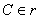 in modo che
il triangolo in modo che
il triangolo 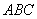 abbia area abbia area 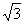 . .
|
|
Determinare la posizione reciproca delle due rette
|
Scrivere l’equazione cartesiana del piano 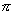 parallelo
alle due rette parallelo
alle due rette 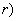 ed ed 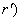 e passante per il punto e passante per il punto 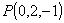 . .
|
|
.
|
Scrivere
le equazioni della retta parallela al vettore 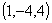 e incidente entrambe le rette e incidente entrambe le rette
|
|
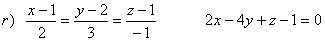
|
Trovare l’equazione
del piano passante per la retta r) e perpendicolare al piano di equazione 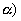 . .
|
|
|
Calcolare la
distanza dell’origine del sistema cartesiano dalla retta di equazioni
|
|
|
Dato il punto 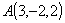 e la retta. e la retta.
determinare per
quale valore di 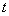 è minima la distanza di è minima la distanza di 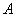 da un punto da un punto 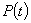 della retta della retta 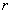 al variare
di al variare
di 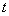 . .
|