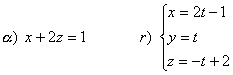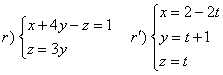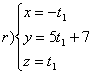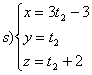Verificare che la retta  e il piano

sono paralleli e calcolare la distanza della retta  dal piano .

.

Scrivere le equazioni della retta parallela al vettore  e incidente entrambe le rette

Verificare che le due rette r,s

sono sghembe e calcolare la distanza dell’origine O dalle due rette.

Sia  r) la retta di equazione

.

Determinare :

a) il piano che contiene r) e il punto P(1,0,2);

b) il piano che contiene r) ed è ortogonale al piano  x + 2y = 0.

Verificare che le rette di equazioni

sono parallele e distano tra loro .

Assegnate le equazioni delle due rette

determinare se sono sghembe, e se lo sono calcolare la retta di minima distanza.

Assegnate le equazioni delle due rette

si chiede: sono sghembe? sono perpendicolari?

Determinare il piano per l’origine parallelo ad esse.

Dato il punto  e le rette r), si chiede di determinare l’equazione

del piano  passante per  parallelo ad  e ad  .

Date le rette ,  e il piano  di equazione: , determinare il piano passante per  e per il punto d’intersezione di  con .

.

.

Data la retta r)

Calcolare l’equazione cartesiana del piano

passante per  e per il punto .

Calcolare l’equazione cartesiana del piano

 parallelo al piano  e passante per il punto

Data la retta r)

Calcolare l’equazione cartesiana del piano

passante per  e per il punto .

Calcolare l’equazione cartesiana del piano

parallelo al piano  e passante per il punto .

       .

Sia dato il punto  di coordinate .

Determinare l’equazione del piano  

passante per il punto  e contenente la retta  r)

Determinare le coordinate del punto Q in comune tra la retta  s)

Determinare l’equazione della retta, contenuta in , passante per  P  e incidente la retta s).

Determinare il piano parallelo ai vettori

e passante per il punto .

Clicca qui

Date le equazioni delle due rette r) s) determinare se sono incidenti parallele o sghembe

,

.

Determinare l’equazione della retta  del piano α) incidente la retta r) e ortogonale alla retta s)

Determinare l’equazione del piano  perpendicolare al piano α)

parallelo alla retta r) e che passa per il punto di coordinate .

Clicca qui

Nello spazio S₃ , riferito a un sistema cartesiano ortonormale, sono dati

Þ il punto A(0, 0, 1),

Þ il punto B(1, 2, 0),

Þ la retta  r .

)          ).

Determinare l’equazioni della retta che  passa per , appartiene al piano  ed è incidente la retta )

)            ).

Determinare l’equazioni della retta ) che

passa per , è parallela al piano ,

ed è incidente la retta )

)         .

Determinare le equazioni della retta  parallela al piano  di equazione:

ortogonale e incidente la retta  di equazioni

e incidente la retta

HOME PAGE

LINK UTILI

AUTORI

SCRIVETECI